Impulse Train in SuperCollider

In SuperCollider there are no readily available UGens for creating a fixed number of single sample impulses. One could cobble something together using Demand rate UGens...

(
c = {|dur = 1, num = 8|
  Duty.ar(Dseq([SampleDur.ir, dur / num - SampleDur.ir], inf), 0, Dseq([1, 0], num));
}.play(fadeTime: 0);
)

or another variant could be to use a combination of Sweep and Changed...

(
c= {|dur = 1, num = 8|
  Changed.ar(Sweep.ar(0, num / dur).ceil.min(num));
}.play(fadeTime:0);
)

but there is a more flexible technique using an envelope. The big win doing it like this is that we can play with the envelope's curvature and get different shapes.

//impulse train with curvature
(
c = {|
  t_go, // trigger
  dur = 1, // total duration in seconds (also frequency)
  cur = 0, // curvature or 'shape'. 0 = pulses at regular intervals
  num = 8, // number of impulses per duration
  amp = 1|
  var env = EnvGen.ar(Env(#[0, 0, 1], [0, dur], cur), t_go);
  var train = Changed.ar(ceil(env * num)) * amp;
  // train = train * (1 - env); // optional decreasing amplitude
  // train = train * env; // optional - increasing amplitude
  train;
}.play;
)
c.set(\t_go, 1);
c.set(\t_go, 1, \cur, 3, \num, 18); // start slow and go faster
c.set(\t_go, 1, \cur, -2, \num, 18); // slower and slower
c.set(\amp, 0.2);
c.set(\t_go, 1, \cur, 0, \dur, 0.5, \num, 200); // 200 for half a second = 400 Hz

The trick to converting an envelope into discrete impulses is to make the linear 0-1 ramp into whole number steps (scale up with * num and run it through ceil) and then trigger an impulse each time the step changes (using the Changed UGen). Then multiplying the train of impulses with the original envelope is optional. The extra multiplication will fade in or fade out the amplitude over the given duration.

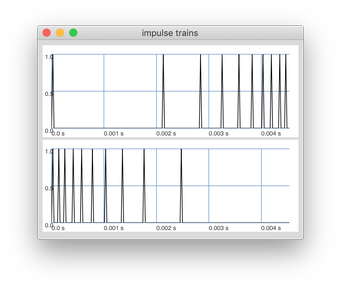
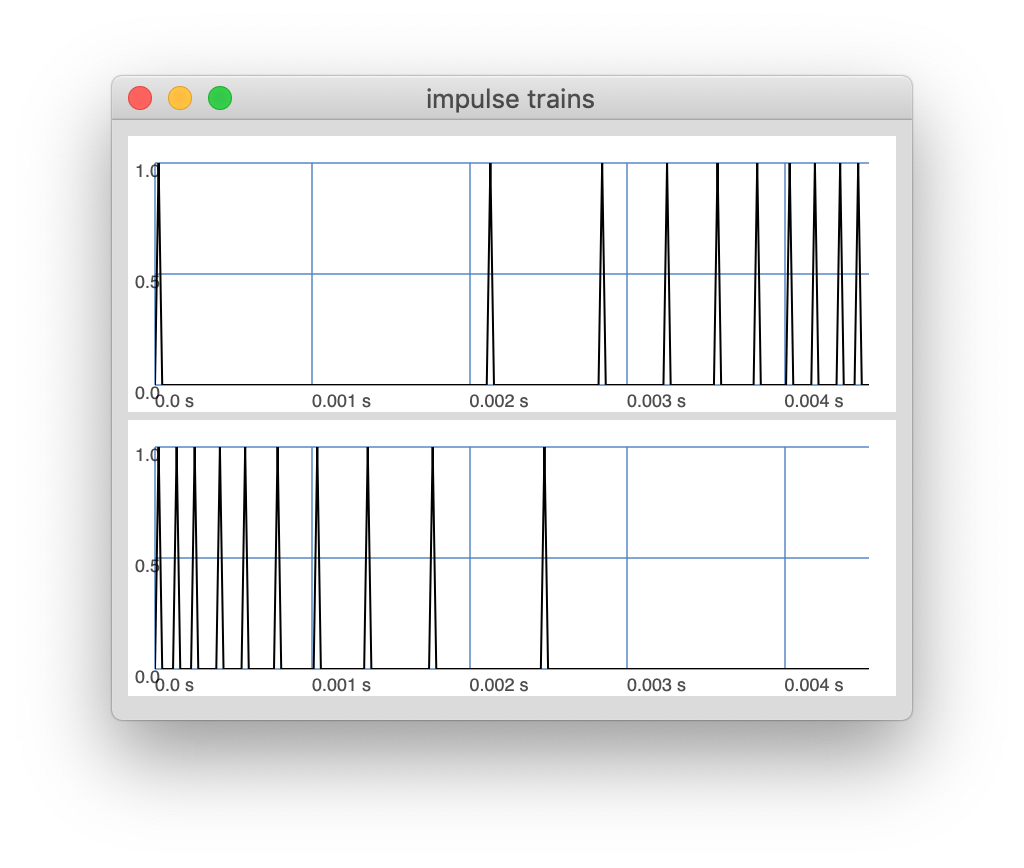
The plot below shows two short bursts. There are 10 impulses spread over 200 samples at a sample rate of 44.1KHz. The top one has its curvature set to 4 and thereby the impulse train gets exponentially faster. In the bottom plot, the curvature is the inverse -4 and thereby the train starts fast and then slows down.

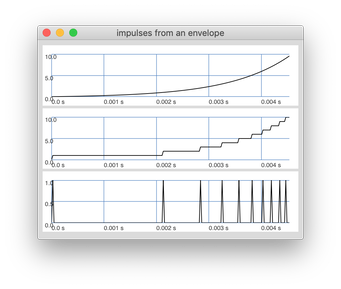
And here is the same (top) impulse train again but showing the process from the curved envelope, via the discrete steps and to the resulting impulses.